Orthorhombic crystal system

In crystallography, the orthorhombic crystal system is one of the seven lattice point groups. Orthorhombic lattices result from stretching a cubic lattice along two of its orthogonal pairs by two different factors, resulting in a rectangular prism with a rectangular base (a by b) and height (c), such that a, b, and c are distinct. All three bases intersect at 90° angles. The three lattice vectors remain mutually orthogonal.
Contents |
Bravais Lattices
There are four orthorhombic Bravais lattices: simple orthorhombic, base-centered orthorhombic, body-centered orthorhombic, and face-centered orthorhombic.
| simple orthorhombic | base-centered orthorhombic |
body-centered orthorhombic |
face-centered orthorhombic |
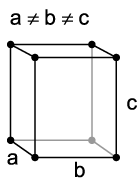 |
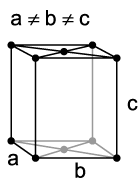 |
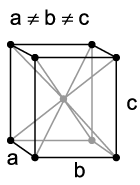 |
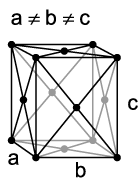 |
Crystal Classes
The orthorhombic crystal system class names, examples, Schönflies notation, Hermann-Mauguin notation, point groups, International Tables for Crystallography space group number[1], orbifold, type, and space groups are listed in the table below.
| Crystal Class | Example | Schönflies | Hermann-Mauguin notation | point groups | # | orbifold | Type | space groups | |||||||
| bipyramidal [2] | olivine, aragonite | D2h | mmm | 47-74 | *222 | centrosymmetric | Pmmm, Pnnn, Pccm, Pban, Pmma, Pnna, Pmna, Pcca, Pbam, Pccn, Pbcm, Pnnm, Pmmn, Pbcn, Pbca, Pnma, Cmcm, Cmce, Cmmm, Cccm, Cmme, Ccce, Fmmm, Fddd, Immm, Ibam, Ibca, Imma | ||||||||
| pyramidal [2] | hemimorphite, bertrandite | C2v | mm2 | 25-46 | *22 | polar | Pmm2, Pmc21, Pcc2, Pma2, Pca21, Pnc2, Pmn21, Pba2, Pna21, Pnn2, Cmm2, Cmc21, Ccc2, Amm2, Aem2, Ama2,Aea2, Fmm2, Fdd2, Imm2, Iba2, Ima2 | ||||||||
| sphenoidal [2] | epsomite | D2 | 222 | 16-24 | 222 | enantiomorphic | P222, P2221, P21212, P212121, C2221, C222, F222, I222, I212121 | ||||||||
See also
- Crystal structure
- Overview of all space groups
References
- Hurlbut, Cornelius S.; Klein, Cornelis, 1985, Manual of Mineralogy, 20th ed., pp. 69 - 73, ISBN 0-471-80580-7
- ↑ Prince, E., ed (2006). International Tables for Crystallography. International Union of Crystallography. doi:10.1107/97809553602060000001. ISBN 978-1-4020-4969-9.
- ↑ 2.0 2.1 2.2 "The 32 crystal classes". http://www.cartage.org.lb/en/themes/sciences/physics/SolidStatePhysics/AtomicBonding/CrystalStructure/32Crystal/32Crystal.htm. Retrieved 2009-07-08.
|
|||||